🏆2025春季走美杯数学竞赛真题含解析-六年级
创建时间:2025-09-27 15:59:16
年份:2025
年级:六年级
杯赛:走美杯
描述:从筛选结果创建的官方真题
题号140
中等
应用题
第4题【单选题】
甲以每小时 6 千米的速度步行从 A 地前往 B 地,在甲出发 90 分钟后,乙发现甲落下了重要物品,立即骑自行车以每小时 12 千米的速度追甲,终于在上午 11 点时追上了甲。甲出发时间是 ( )
题号141
中等
几何图形
第5题【单选题】
七巧板是一种智力游戏,是由七块板组成的。由于等积变换,所以这七块板可拼成许多图形 (千种以上),如图所示。如果七块板组成的正方形边长是 4,那么除此之外,用这些七巧板还可以拼出的正方形边长可能有几种情况?( )


题号142
中等
计算技巧
第6题【填空题】
已知
\( a■b=10 \)
,
\( a*2b=12 \)
,其中■*是四则运算符,且 a、b 均为正整数,那么 a 可能的数值有________;* 的运算符不可能是________。
题号143
中等
几何图形
第7题【填空题】
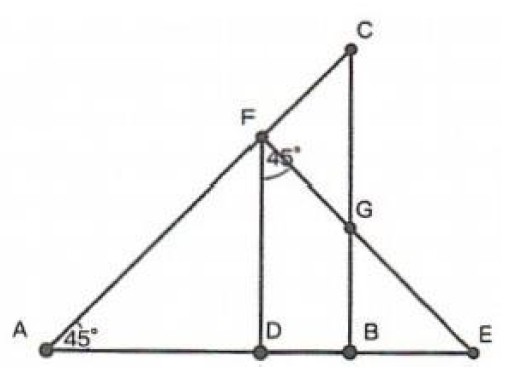
有一大一小两个等腰三角形直尺,按照如图方式叠放,已知大三角形的直角边是 10,小三角形的直角边是 8。那么:(1) 重叠部分 BDFG 的面积是________;(2) 叠放之后所形成的图形 AEGC 的面积是________。

题号146
中等
几何图形
第10题【填空题】
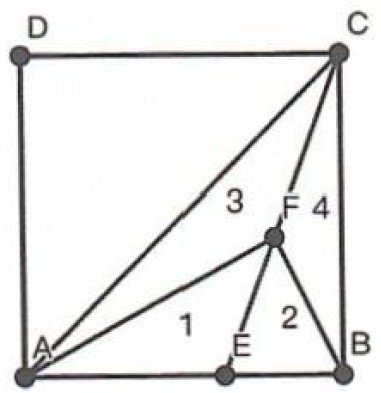
四个孩子分一个 450 克的蛋糕 (如图所示,ABCD 为正方形)。小蓝、小绿、小黄、小红各切了一刀,他们把最大的一块 (ACD) 留给了爸爸妈妈。小绿拿了 3,约 63 克;小蓝拿了 4,约 27 克。如果小红拿了 1,小黄拿了 2,那么小红的蛋糕为________克,小红与小黄的蛋糕相差了________克。

题号149
中等
数论初步
第13题【填空题】
“走进美妙数学花园” 活动起源于 2002 年第 24 届世界数学家大会,今年是 2025 年,2002~2025 这几个年份数字中,有________个质数。
题号150
困难
计算技巧
第14题【填空题】
斐波那契数列,又称黄金分割数列,因数学家莱昂纳多・斐波那契 (Leonardo Fibonacci) 以兔子繁殖为例子而引入,故又称 “兔子数列”,其数值为:0、1、1、2、3、5、8、13、21…… 这个数列从第 3 项开始,每一项都等于前两项之和,那么数列中:(1) 前 2025 项中有多少个奇数?(2) 第 2025 个奇数是第几项?
题号151
困难
数论初步
第15题【填空题】
用 1,2,3,4,6,7,8,9 这 8 个数字组成一个多位整数,使这个数能被 1,2,3,4,6,7,8,9 中的每个数整除,其中每个数字至少使用 1 次,也可以重复使用,例如 6468319322。这样的整数中,最小的数是________。