本题目所在的杯赛真题试卷:
🏆2025春季走美杯数学竞赛真题含解析-六年级
六年级
走美杯
2025
中等
几何图形
几何模型(等高模型、鸟头模型、蝴蝶模型等)
题目内容
题146【填空题】
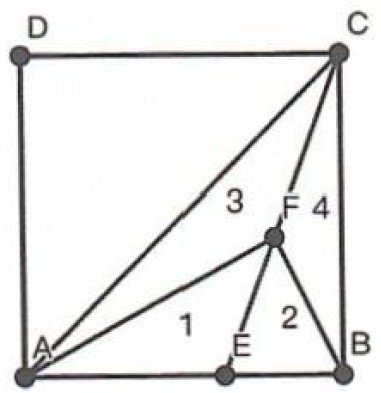
四个孩子分一个 450 克的蛋糕 (如图所示,ABCD 为正方形)。小蓝、小绿、小黄、小红各切了一刀,他们把最大的一块 (ACD) 留给了爸爸妈妈。小绿拿了 3,约 63 克;小蓝拿了 4,约 27 克。如果小红拿了 1,小黄拿了 2,那么小红的蛋糕为________克,小红与小黄的蛋糕相差了________克。

参考答案
\( 94.5 \)
;
\( 54 \)
题目解析
根据燕尾模型,1 与 2 的面积之比和 3 与 4 的面积之比相同,故 1 与 2 的重量之比也为
\( 63:27=7:3 \)
。蛋糕留给孩子的部分重量为
\( 450÷2 - 63 - 27=135 \)
克。设小红的蛋糕重量为 7x 克,小黄的为 3x 克,则
\( 7x + 3x=135 \)
,解得 x=13.5。所以小红的蛋糕重量为
\( 7×13.5=94.5 \)
克,小黄的为
\( 3×13.5=40.5 \)
克,两者相差
\( 94.5 - 40.5=54 \)
克