第1题【填空题】 算式 \( (20 ×2-5) ÷\frac {1}{11} \) 的计算结果是__________。

第2题【填空题】 哈利波特拥有一瓶聪明药。在准备第一场考试时，他喝了药水的 \( \frac {1}{4} \) , 此时药水和瓶子的总重量为 110 克；在准备二场考试前，他又喝了剩下的 \( \frac {2}{3} \) , 此时药水和瓶子的总重量为 50 克。那么，原来这瓶聪明药水共有_________克.

第3题【填空题】 小明计划绘制一个具有小太阳笑脸特征的图案。为此，他首先绘制了一个边长为 10 的正十二边形，再以该正十二边形的每个顶点为圆心，边长的一半为半径，画 12 个扇形，这些扇形共同构成如图所示的 “太阳” 轮廓。那么，这个 “太阳” 轮廓的总长度是_________.(π 取 3.14)

第4题【填空题】 有四个互不相同的质数 a 、 b 、 c 、 d , 满足 \( (a+b) ×(a+c) ×(a+d)=2025 \) , 那么 \( a+b+c+d= \) _________

第5题【填空题】 在一个 \( 10×10 \) 的初始全为白色的棋盘上，甲和乙两人进行染色游戏。首先，甲选择 n 个格子染成红色：接着，乙染 4 行 4 列黑色。如果游戏结束时，棋盘上至少还剩下一个红色格子，则判定甲胜利，否则判定乙胜利。那么，当 n 最小值为_________时，甲能确保有必胜策略.

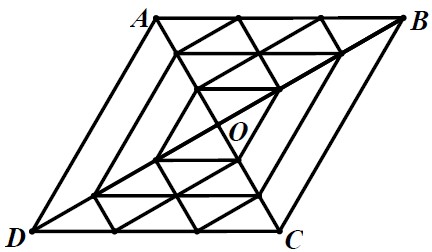
第6题【填空题】 如图，在平行四边形 ABCD 中，分别在 OA 、 OB 、 OC 、 OD 以及 AB 、 CD 上取三等分点并连接，那么图中一共可以构成_________个平行四边形.

第7题【填空题】 一个三位数除以 63、84、145 所得的三个余数之和恰好等于该数本身，那么这个三位数是_________

第8题【填空题】 老师与甲、乙两名同学共同进行一场游戏。游戏规则如下：老师先在黑板上写一个小于 2025 的正整数；甲先将这个数擦掉，然后将这个数的 2 倍写在黑板上；乙接着将甲写的数擦掉，再将甲写的数与 100 的和写在黑板上。游戏按照 “甲 - 乙 - 甲 - 乙 -…” 的顺序轮流进行，直到某位同学首次在黑板上写出一个大于 2025 的数，则该同学获胜。如果最终乙同学获胜，那么，老师在黑板上最初书写的数最小可能是_________

第9题【填空题】 如图，正六边形中两个阴影部分面积分别是 20 和 25, 那么正六边形的面积是_________

第10题【填空题】 早上 8:00, 甲车从 A 地出发前往 B 地，同时乙车、丙车从 B 地出发前往 A 地，C 地是 AB 两地的中点。已知 10:00 时，甲、乙两车相遇；11:00 时，甲车未到达 B 地且在 BC 两地之间，丙车恰好处于甲车和 C 地的中点；乙车到达 A 地后调头与丙车相遇时，乙车一共走了 300 千米。那么 AB 两地之间的距离是_________千米.(不考虑车身长度)

第11题【填空题】 甲、乙、丙、丁、戊五人面前分别放置了浓度分别为 10%、20%、30%、40%、50% 的五瓶酒精溶液，同时旁边还有一瓶重 25 克的清水。这五人依次从各自正面前的酒精溶液中取出 a、b、c、d、e 克滴入清水瓶中。最终，清水瓶中的酒精浓度变为了 15%. 已知 a、b、c、d、e 都是一位数奇数，且互不相同；乙取出的酒精溶液既不是最多的，也不是最少的，但比甲取出的要少。那么五位数 abcde 是_________

第12题【填空题】 你认为本试卷中一道最佳试题是第________题（答题范围为01～11、13、14）；
你认为本试卷整体的难度级别是________（最简单为“1”，最难为“9”，答题
范围为1～9）；
你认为本试卷中一道最难试题是第________题（答题范围为01～11、13、14）．
（所有答题范围内的作答均可得分，所有的评定都将视为本人对本试卷的
有效评定，不作答或者超出作答范围不得分．）

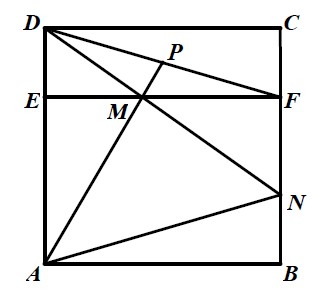
第13题【问答题】 如图，长方形 ABFE 和长方形 CDEF 拼接成了正方形 ABCD , 点 P 是 DF 的中点，AP 与 EF 交于 M , DM 与 BC 交于 N . 已知 EM=FN , 三角形 AEM 的面积是 2025。
1) 请求出△ABN 的面积；(6 分)
2) 请求出△AMN 的面积.(9 分)

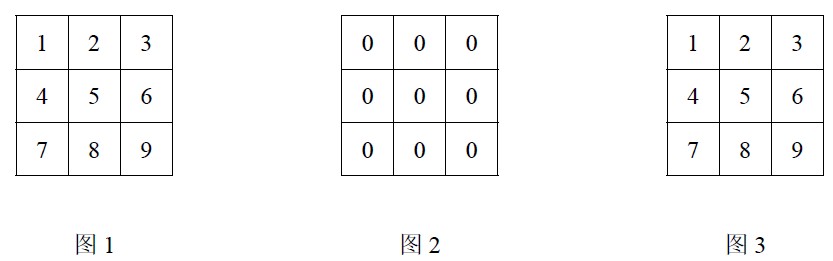
第14题【问答题】 对于一个给定的方格表，每次操作可以选择以下图中四种模式之一，将所选模式中的三个格子内的数同时加 1。

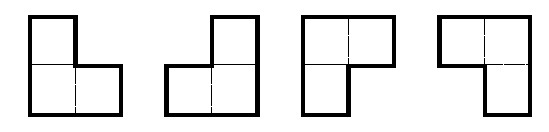
(1) 如图 1, 至少需要操作_________次，才能使每个格子内的数的奇偶性都相同，请直接给出答案；(3 分)
(2) 如图 2, 至少需要操作多少次，才能使每个格子内的数都变成奇数？请描述具体的操作方法；(6 分)
(3) 如图 3, 能否通过若干次操作，使所有格子内的数变成相同的数？请说明理由.(6 分)