本题目所在的杯赛真题试卷:
🏆2025迎春杯数学花园探秘小高年级决赛C卷
六年级
迎春杯
2025
困难
几何图形
立体几何(表面积与体积)
题目内容
题208【问答题】
如图,长方形 ABFE 和长方形 CDEF 拼接成了正方形 ABCD , 点 P 是 DF 的中点,AP 与 EF 交于 M , DM 与 BC 交于 N . 已知 EM=FN , 三角形 AEM 的面积是 2025。
1) 请求出△ABN 的面积;(6 分)
2) 请求出△AMN 的面积.(9 分)
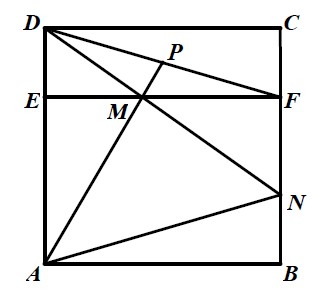
1) 请求出△ABN 的面积;(6 分)
2) 请求出△AMN 的面积.(9 分)

参考答案
(1)2025;(2)4050
题目解析
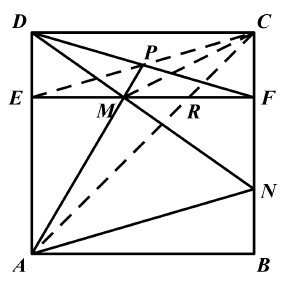
(1) 分别连接 CE、CM、CA,在正方形 ABCD 中,CA 是对角线,则 CF=FR,因为 EM=FN,所以 MR=BN,故
\( S_{\triangle MAC}=S_{\triangle BNA} \)
,在长方形 DFCD 中,点 P 是 CE 的中点,则 EP=PC,所以
\( S_{\triangle BNA}=S_{\triangle MAC}=S_{\triangle EMA}=2025 \)
;
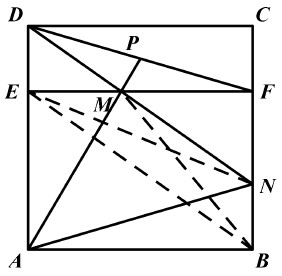
(2) 分别连接 BE、BM、EN,因为 \( S_{\triangle EMB}=S_{\triangle EMA}=S_{\triangle BNA}=S_{\triangle BNE} \) ,所以 EB//DN,则四边形 DEBN 是平行四边形,故 \( BN=DE=CF \) ,所以 \( FM=2BN \) ,因为 \( S_{ABFE}=S_{\triangle AMN}+S_{\triangle AME}+S_{\triangle ABN}+S_{\triangle FMN}=S_{\triangle AMN}+4050+\frac {1}{2}×FM×FN \) , \( S_{ABFE}=2S_{AMN}+EM×BN \) ,所以 \( S_{\triangle AMN}+4050+\frac {1}{2}×FM×FN=2S_{\triangle AMN}+EM×BN \) ,即 \( S_{\triangle AMN}=4050 \)

(2) 分别连接 BE、BM、EN,因为 \( S_{\triangle EMB}=S_{\triangle EMA}=S_{\triangle BNA}=S_{\triangle BNE} \) ,所以 EB//DN,则四边形 DEBN 是平行四边形,故 \( BN=DE=CF \) ,所以 \( FM=2BN \) ,因为 \( S_{ABFE}=S_{\triangle AMN}+S_{\triangle AME}+S_{\triangle ABN}+S_{\triangle FMN}=S_{\triangle AMN}+4050+\frac {1}{2}×FM×FN \) , \( S_{ABFE}=2S_{AMN}+EM×BN \) ,所以 \( S_{\triangle AMN}+4050+\frac {1}{2}×FM×FN=2S_{\triangle AMN}+EM×BN \) ,即 \( S_{\triangle AMN}=4050 \)

视频解析
None