本题目所在的杯赛真题试卷:
🏆2025迎春杯数学花园探秘小高年级决赛C卷
六年级
迎春杯
2025
困难
逻辑推理
操作与策略问题(如必胜策略)
题目内容
题209【问答题】
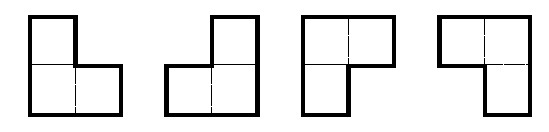
对于一个给定的方格表,每次操作可以选择以下图中四种模式之一,将所选模式中的三个格子内的数同时加 1。
(1) 如图 1, 至少需要操作_________次,才能使每个格子内的数的奇偶性都相同,请直接给出答案;(3 分)
(2) 如图 2, 至少需要操作多少次,才能使每个格子内的数都变成奇数?请描述具体的操作方法;(6 分)
(3) 如图 3, 能否通过若干次操作,使所有格子内的数变成相同的数?请说明理由.(6 分)
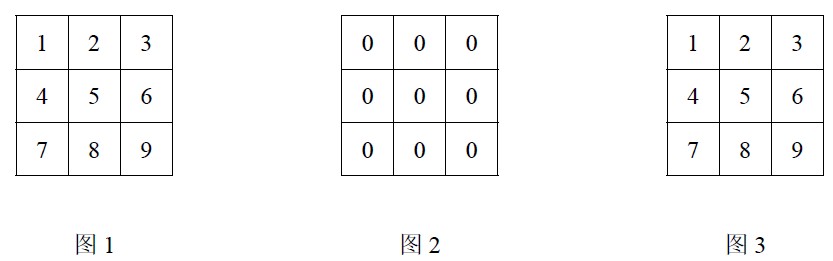

(1) 如图 1, 至少需要操作_________次,才能使每个格子内的数的奇偶性都相同,请直接给出答案;(3 分)
(2) 如图 2, 至少需要操作多少次,才能使每个格子内的数都变成奇数?请描述具体的操作方法;(6 分)
(3) 如图 3, 能否通过若干次操作,使所有格子内的数变成相同的数?请说明理由.(6 分)

参考答案
(1) 2 次;(2) 5 次;(3) 不能
题目解析
(1) 按对应模式操作即可;
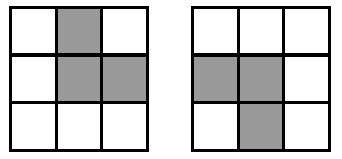
(2) 四个角格都至少被操作一次,故操作次数≥4,每个格子的奇偶性都改变,即所有格子中的数之和是奇数,每次操作总和 + 3,所以操作次数是奇数,即操作次数至少是 5 次,按对应模式操作即可;

(3) 按中心格、边格、角格进行分类,最初的状态:中心格是 5,边格数之和是 20,角格数之和是 20,如果最终 9 个格子中的数都变成了 T,那么中心格是 T,边格数之和是 \( 4T \) ,角格数之和是 \( 4T \) ,每一次操作对中心格、边格、角格的影响如下:
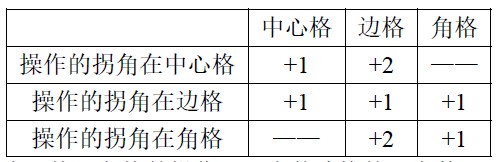
一旦进行了拐角在中心格或角格的操作,就会使边格的四个数之和大于角格的四个数之和,为了确保边格数之和和角格数之和相等 (都是 4T),只能做拐角在边格的操作,进行了 m 次拐角在边格的操作后, \( \frac {中心数}{边格之和}=\frac {5+m}{20+m}>\frac {1}{4} \) ,即在中心格为 T 时,边格数之和不可能是 \( 4T \) ,综上,不能变成相同的数

(2) 四个角格都至少被操作一次,故操作次数≥4,每个格子的奇偶性都改变,即所有格子中的数之和是奇数,每次操作总和 + 3,所以操作次数是奇数,即操作次数至少是 5 次,按对应模式操作即可;

(3) 按中心格、边格、角格进行分类,最初的状态:中心格是 5,边格数之和是 20,角格数之和是 20,如果最终 9 个格子中的数都变成了 T,那么中心格是 T,边格数之和是 \( 4T \) ,角格数之和是 \( 4T \) ,每一次操作对中心格、边格、角格的影响如下:

一旦进行了拐角在中心格或角格的操作,就会使边格的四个数之和大于角格的四个数之和,为了确保边格数之和和角格数之和相等 (都是 4T),只能做拐角在边格的操作,进行了 m 次拐角在边格的操作后, \( \frac {中心数}{边格之和}=\frac {5+m}{20+m}>\frac {1}{4} \) ,即在中心格为 T 时,边格数之和不可能是 \( 4T \) ,综上,不能变成相同的数
视频解析
None