🏆2025年19届-时代杯-真题-6年级
创建时间:2025-10-11 02:09:14
年份:2025
年级:六年级
杯赛:时代杯
描述:从筛选结果创建的官方真题
题号244
中等
计算技巧
第1题【填空题】
神机妙算 计算下面各题。
(1) \( \frac {9}{10} \div\left (\frac {1}{4} \times\left (\frac {6}{5}-\frac {1}{3}\right)\right) \) =_________
(2) \( \frac{1}{45} × 3 \frac{1}{7}+\frac{22}{63} ÷ 3 \frac{3}{14}+\frac{34}{45} × \frac{46}{63} \) =_________
(3) \( \frac{3}{1 × 2}-\frac{5}{2 × 3}+\frac{7}{3 × 4}-\frac{9}{4 × 5}+\cdots+\frac{199}{99 × 100}-\frac{201}{100 × 101} \) =_________
(4) \( \frac{1}{1^{3}}+\frac{1+2}{1^{3}+2^{3}}+\frac{1+2+3}{1^{3}+2^{3}+3^{3}}+\cdots+\frac{1+2+3+\cdots+2025}{1^{3}+2^{3}+3^{3}+\cdots+2025^{3}} \) =_________
(1) \( \frac {9}{10} \div\left (\frac {1}{4} \times\left (\frac {6}{5}-\frac {1}{3}\right)\right) \) =_________
(2) \( \frac{1}{45} × 3 \frac{1}{7}+\frac{22}{63} ÷ 3 \frac{3}{14}+\frac{34}{45} × \frac{46}{63} \) =_________
(3) \( \frac{3}{1 × 2}-\frac{5}{2 × 3}+\frac{7}{3 × 4}-\frac{9}{4 × 5}+\cdots+\frac{199}{99 × 100}-\frac{201}{100 × 101} \) =_________
(4) \( \frac{1}{1^{3}}+\frac{1+2}{1^{3}+2^{3}}+\frac{1+2+3}{1^{3}+2^{3}+3^{3}}+\cdots+\frac{1+2+3+\cdots+2025}{1^{3}+2^{3}+3^{3}+\cdots+2025^{3}} \) =_________
题号245
中等
应用题
第2题【填空题】
南极昼长 1985 年 2 月 15 日,中国第一个南极考察站 -- 长城站在南极洲乔治岛建成。下面示意图为某年长城站各月最长昼长 (单位:小时)。
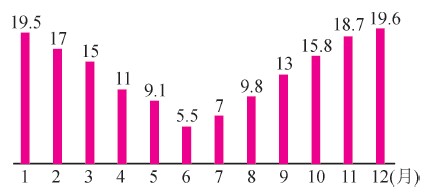
(1)_________月最长昼长最长,达到_________小时;_________月最短夜长最长,达到_________小时。
(2) 7 月的最长昼长比 3 月短_________%(百分号前保留一位小数)
(3) 南极洲每年只分两季:寒季和暖季。南极洲一年中有连续 7 个月的寒季,寒季中最中间的一个月是最长昼长第二短的那个月。春节期间长城站处于_________(A) 寒季 (B) 暖季

(1)_________月最长昼长最长,达到_________小时;_________月最短夜长最长,达到_________小时。
(2) 7 月的最长昼长比 3 月短_________%(百分号前保留一位小数)
(3) 南极洲每年只分两季:寒季和暖季。南极洲一年中有连续 7 个月的寒季,寒季中最中间的一个月是最长昼长第二短的那个月。春节期间长城站处于_________(A) 寒季 (B) 暖季
题号246
中等
数学思想与方法
第3题【填空题】
火眼金睛 选择正确的选项填在括号里。
(1) 如何从自然数中挑选出素数?一位古希腊数学家把自然数列成一张数表,再按规则逐个划去不是素数的自然数。这种找素数的方法叫作 (_________)筛法。
(A) 阿基米德 (B) 泰勒斯 (C) 埃拉托塞尼
(2)“方田术曰:广从步数相乘得积步。以亩法二百四十步除,即亩数。” 这段描述最可能出自 (_________)
(A)《九章算术》(B)《几何原本》(C)《黄帝内经》
(3) 以下不属于古希腊三大几何作图难题的是 (_________)
(A) 化圆为方 (B) 尺规作正十七边形 (C) 三等分任意角
(1) 如何从自然数中挑选出素数?一位古希腊数学家把自然数列成一张数表,再按规则逐个划去不是素数的自然数。这种找素数的方法叫作 (_________)筛法。
(A) 阿基米德 (B) 泰勒斯 (C) 埃拉托塞尼
(2)“方田术曰:广从步数相乘得积步。以亩法二百四十步除,即亩数。” 这段描述最可能出自 (_________)
(A)《九章算术》(B)《几何原本》(C)《黄帝内经》
(3) 以下不属于古希腊三大几何作图难题的是 (_________)
(A) 化圆为方 (B) 尺规作正十七边形 (C) 三等分任意角
题号247
中等
数论初步
第4题【填空题】
推出 “文化节” 下面算式中相同的汉字代表相同的数字,不同的汉字代表不同的数字。(“文化节” 表示一个三位数)
\( 2025 ÷ \frac {文化节}{文 + 化 + 节}= 文化节 \) , 那么文 =_________, 化 =_________, 节 =_________
\( 2025 ÷ \frac {文化节}{文 + 化 + 节}= 文化节 \) , 那么文 =_________, 化 =_________, 节 =_________
题号248
中等
几何图形
第5题【填空题】
足球模型 你注意到了吗?生活中常见的足球是一种美妙的几何体。它不仅被用来进行艺术设计,还可以作为分子结构模型。
这种几何体由 12 个五边形和 20 个六边形围成,每个顶点都是 1 个五边形和 2 个六边形的公用顶点,则它的表面一共有_________条棱 (边),_________个顶点。

这种几何体由 12 个五边形和 20 个六边形围成,每个顶点都是 1 个五边形和 2 个六边形的公用顶点,则它的表面一共有_________条棱 (边),_________个顶点。

题号249
简单
应用题
第6题【填空题】
混合调色 美术课上,王老师用白色和黑色两种颜料混合调出灰色,调出效果的色卡如下图。
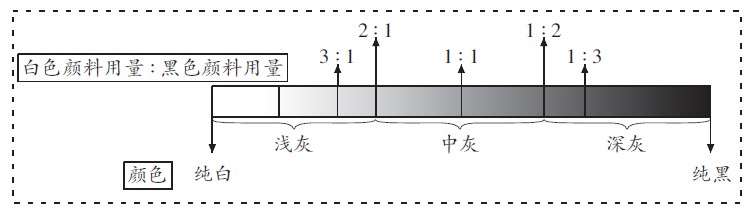
白色颜料用量∶黑色颜料用量 3∶1、1∶1、1∶3,颜色对应浅灰、中灰、深灰、纯黑。美术老师给大家出了一个数学题:黑色颜料用量是白色颜料用量的 40% 时,调出的颜色属于_________色。

白色颜料用量∶黑色颜料用量 3∶1、1∶1、1∶3,颜色对应浅灰、中灰、深灰、纯黑。美术老师给大家出了一个数学题:黑色颜料用量是白色颜料用量的 40% 时,调出的颜色属于_________色。
题号250
中等
应用题
第7题【填空题】
运输损耗 某批发商订购了 12 吨车厘子,在运输过程中,所含水分从原先的 90% 降到 85%, 这批车厘子到达目的地时是_________吨。
题号251
中等
应用题
第8题【填空题】
巧算营员 小时参加《时代学习报》冬季拓展营。冬季拓展营有 A,B,C 三个班。三个班的人数依次增多相同的数量。若全体学员人数为 240 人,其中 30% 的女学员与 25% 的男学员在 A 班,25% 的女学员与 35% 的男学员在 B 班,那么冬季拓展营中,男学员一共有_________人。
题号252
中等
计数与组合
第9题【填空题】
连排空位 小时、小代和小报一起去电影院观看《哪吒之魔童闹海》, 刚好有 6 个空座位连成一排。现在 3 人就座,恰好有 2 个空座位相邻的不同坐法有_________种。
题号253
中等
计算技巧
第10题【填空题】
分数拆分 观察下面的算式,回答问题。
\( \frac {1}{3 × 4}+\frac {1}{4}=\frac {1+3}{3 × 4}=\frac {1}{3} \)
,
\( \frac {1}{4 × 5}+\frac {1}{5}=\frac {1+4}{4 × 5}=\frac {1}{4} \)
…… 找出自然数 x,y, 满足
\( x>y \)
,且
(1) \( \frac {1}{x}+\frac {1}{y}=\frac {1}{23} \) ,x=_________,y=_________
(2) \( \frac{1}{x}+\frac{1}{y}=\frac{4}{23} \) ,x=_________,y=_________
(1) \( \frac {1}{x}+\frac {1}{y}=\frac {1}{23} \) ,x=_________,y=_________
(2) \( \frac{1}{x}+\frac{1}{y}=\frac{4}{23} \) ,x=_________,y=_________
题号254
中等
几何图形
第11题【填空题】
展开图上的 2025 明明把一个正方体纸盒的表面沿着某些棱剪开后展成一个平面图形 (如下图)。
如果这个正方体的每两个相对面上的数的和都是 2025, 那么 x+y+z=_________
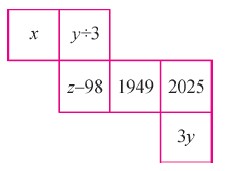
如果这个正方体的每两个相对面上的数的和都是 2025, 那么 x+y+z=_________
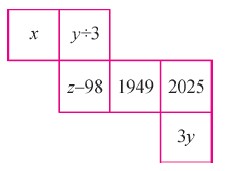
题号255
中等
应用题
第12题【填空题】
套圈追及 小时和小代绕着 400 米的圆形跑道跑步。他们同时从同一地点同向起跑,小时的速度比小代快 25%。当小时第一次从后面追上小代 (俗称 “套圈”) 时,小代已经跑了_________圈。
题号256
困难
几何图形
第13题【填空题】
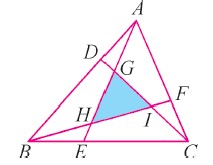
由小见大 如图,在
\( \triangle ABC \)
中,
\( BD=2DA \)
,
\( CE=2EB \)
,
\( AF=2FC \)
。已知阴影三角形的面积是 15 平方厘米,那么
\( \triangle ABC \)
的面积是_________平方厘米。

题号257
中等
逻辑推理
第14题【填空题】
稳操胜券 现有 1~10 这十张数字卡片,小时和小代两人轮流在黑板上贴一张数字卡片,规定不能贴黑板上已有数的约数,最后不能贴者为失败者。如果小时先贴,他要必胜,那么他应该先贴写有数字_________的卡片。
题号258
困难
几何图形
第15题【填空题】
截顶金字塔 埃及金字塔是世界七大建筑奇迹之一。其形状为正四棱锥,底部为正方形,如下左图。正四棱锥的体积 =
\( \frac {1}{3}× 底面积 × 高 \)
。金字塔的建造工程浩大,设计精妙,其中也反映了古埃及的伟大数学成就。
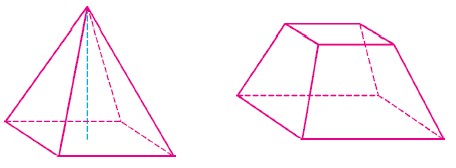
建造金字塔时,首先会建造如上右图的截顶金字塔。计算截顶金字塔的体积,也是古埃及几何的一项最杰出的成就。如果一个截顶金字塔的高为 6 米,上、下底正方形的边长分别为 2 米和 4 米,那么这个截顶金字塔的体积是_________立方米。

建造金字塔时,首先会建造如上右图的截顶金字塔。计算截顶金字塔的体积,也是古埃及几何的一项最杰出的成就。如果一个截顶金字塔的高为 6 米,上、下底正方形的边长分别为 2 米和 4 米,那么这个截顶金字塔的体积是_________立方米。