本题目所在的杯赛真题试卷:
🏆2025年19届-时代杯-真题-6年级
六年级
时代杯
2025
困难
几何图形
立体几何(表面积与体积)
题目内容
题258【填空题】
截顶金字塔 埃及金字塔是世界七大建筑奇迹之一。其形状为正四棱锥,底部为正方形,如下左图。正四棱锥的体积 =
\( \frac {1}{3}× 底面积 × 高 \)
。金字塔的建造工程浩大,设计精妙,其中也反映了古埃及的伟大数学成就。
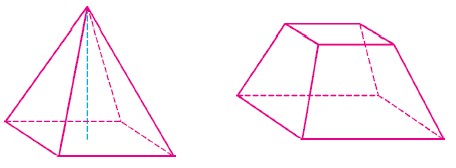
建造金字塔时,首先会建造如上右图的截顶金字塔。计算截顶金字塔的体积,也是古埃及几何的一项最杰出的成就。如果一个截顶金字塔的高为 6 米,上、下底正方形的边长分别为 2 米和 4 米,那么这个截顶金字塔的体积是_________立方米。

建造金字塔时,首先会建造如上右图的截顶金字塔。计算截顶金字塔的体积,也是古埃及几何的一项最杰出的成就。如果一个截顶金字塔的高为 6 米,上、下底正方形的边长分别为 2 米和 4 米,那么这个截顶金字塔的体积是_________立方米。
参考答案
56 立方米
题目解析
向上延长截顶金字塔的侧棱,可得到大小两个正四棱锥。根据上、下底正方形边长的比是 1:2,可知小正四棱锥和大四棱锥的高的比是 1:2。于是可用大四棱锥的体积减去小四棱锥的体积来求截顶金字塔的体积。截顶金字塔的体积 =
\( \frac {1}{3}×4^{2}×6×2-\frac {1}{3}×2^{2}×6=56 \)
立方米
视频解析
None