本题目所在的杯赛真题试卷:
🏆2025年5月第14届海峡杯-全国赛-四年级
四年级
海峡杯
2025
中等
几何图形
几何模型(等高模型、鸟头模型、蝴蝶模型等)
题目内容
题338【问答题】
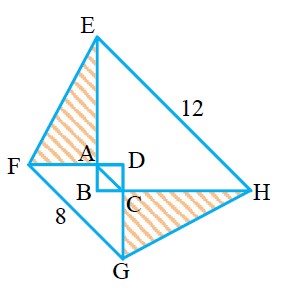
如图,四边形 ABCD 为正方形,△EBH、△FDC 均为等腰直角三角形。其中 AC=2,FG=8,EH=12,求图中阴影部分面积之和。

参考答案
30
题目解析
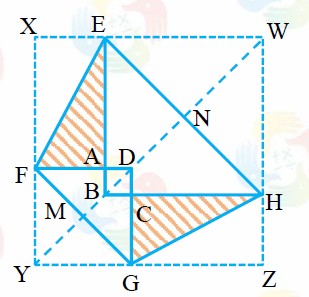
方法一:如图,因为△EBH、△FDG 均为等腰直角三角形,所以四边形 EBHW、FYGD、XYZW 均为正方形。正方形 ABCD 的对角线为 2,面积为
\( 2×2÷2 = 2 \)
。正方形 EBHW 的对角线为 12,面积为
\( 12×12÷2 = 72 \)
。正方形 FYGD 的对角线为 8,面积为
\( 8×8÷2 = 32 \)
。正方形 XYZW 的对角线
\( YW = 12 + 8 - 2 = 18 \)
,面积为
\( 18×18÷2 = 162 \)
。所以,阴影部分面积之和为
\( (162 - 72 - 32 + 2)÷2 = 30 \)
。
方法二:如图,过 B、D 作直线 MN,交 FG 于点 M,交 EH 于点 N。等腰梯形 EFGH 关于 MN 对称,MN 是等腰梯形 EFGH 的高。 \( BD = 2 \) , \( MD = 8÷2 = 4 \) , \( BN = 12÷2 = 6 \) , \( MN = 4 + 6 - 2 = 8 \) 。 \( S_{等腰梯形 EFGH} = (12 + 8)×8÷2 = 80 \) , \( S_{空白} = S_{\triangle EBH} + S_{\triangle GDF} - S_{正方形 ABCD} = 12×6÷2 + 8×4÷2 - 2×2 = 50 \) , \( S_{阴影} = 80 - 50 = 30 \) 。答:图中阴影部分面积之和为 30。
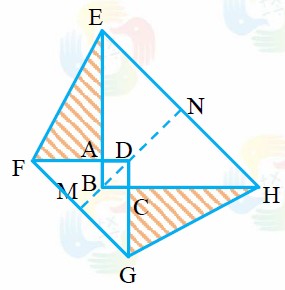

方法二:如图,过 B、D 作直线 MN,交 FG 于点 M,交 EH 于点 N。等腰梯形 EFGH 关于 MN 对称,MN 是等腰梯形 EFGH 的高。 \( BD = 2 \) , \( MD = 8÷2 = 4 \) , \( BN = 12÷2 = 6 \) , \( MN = 4 + 6 - 2 = 8 \) 。 \( S_{等腰梯形 EFGH} = (12 + 8)×8÷2 = 80 \) , \( S_{空白} = S_{\triangle EBH} + S_{\triangle GDF} - S_{正方形 ABCD} = 12×6÷2 + 8×4÷2 - 2×2 = 50 \) , \( S_{阴影} = 80 - 50 = 30 \) 。答:图中阴影部分面积之和为 30。

视频解析
None