由于四人中看见人数最多的那个人说了假话结合甲说的话可知甲说了假话，所以甲看见 2 人，因为其他人看见的人都没有他看见的人多，所以不存在 3 人同一横线或竖线。因此甲与其看见的 2 人（丙和丁）组成一个直角三角形（甲所在的点为直角点），且乙与甲、丙、丁不同横线竖线，根据丁所说任意 3 人所在格点组成的三角形面积都不为整数，可知两条直角边只能为 1 和 1 或者 1 和 3。
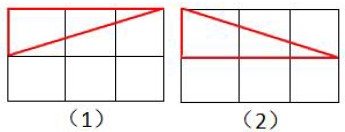
若为1 和1，围城四边形面积最大为2.5。为1 和3 时，当为图（1）形式时，无法构造选择合适的乙使得四边形面积为3，若为图（2）形式时，仅有一个点（第三行第2 个点）满足乙的要求。在画出形如图（2）的图时，甲有2 种，乙的位置有2 种（第一行或第三行），丙、丁站在余下两个点有2 种，可只有2×2×2=8 种站法。