本题目所在的杯赛真题试卷:
🏆2025迎春杯数学花园探秘决赛C卷-小中年级
四年级
迎春杯
2025
困难
计数与组合
题目内容
题234【填空题】
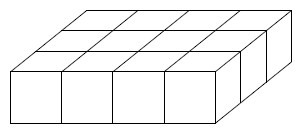
由 12 个相同的小正方体无盖盒子如图摆放,每个盒子内放入若干个相同的球,其球数恰好等于它相邻的盒子中无球的盒子的个数,那么满足要求的放球方式有_________种。(两个盒子有公共顶点、公共边或公共面均视为相邻)

参考答案
22
题目解析
问题转化为一个 3×4 的棋盘填数,每个格子填入的数字为与其相邻的格子中填 0 的个数,依题意,0 与 0 不能相邻,且 0 确定填法其他格子即可唯一确定数值。设第二行中间两个位置 A、B:
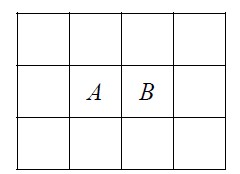
(1)若A 或B 为0,根据对称性不妨假设A 为0,那么与A 相邻的8 个格子均不为0,那么C、D、E 三个格子0 的情况只能是D 为0 或C 和E 同时为0 两种情况,所以共有2×2=4 种。
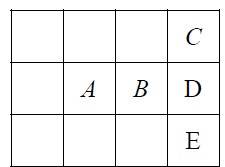
(2)若AB 均不为0 时,将棋盘分成左右两个部分,则每部分最多2 个0,最少1 个0. 按照0 的总数来分类:
若有2 个0: 左右各1 个0,则都只能在第二行,有1 种;
若有3 个0: 左右有一侧有2 个0,则不能在第二行,另一侧只能在第二行,有2×2×2=8 种;
若有4 个0: 左右侧各有2 个0,则都不能在第二行,第一行的两个0有22 1 3种方法,第三行的两个0也有3种放法,共有33 9种;
共有1+8+9=18 种不同放法.
综上,一共4+18=22 种放法。

(1)若A 或B 为0,根据对称性不妨假设A 为0,那么与A 相邻的8 个格子均不为0,那么C、D、E 三个格子0 的情况只能是D 为0 或C 和E 同时为0 两种情况,所以共有2×2=4 种。

(2)若AB 均不为0 时,将棋盘分成左右两个部分,则每部分最多2 个0,最少1 个0. 按照0 的总数来分类:
若有2 个0: 左右各1 个0,则都只能在第二行,有1 种;
若有3 个0: 左右有一侧有2 个0,则不能在第二行,另一侧只能在第二行,有2×2×2=8 种;
若有4 个0: 左右侧各有2 个0,则都不能在第二行,第一行的两个0有22 1 3种方法,第三行的两个0也有3种放法,共有33 9种;
共有1+8+9=18 种不同放法.
综上,一共4+18=22 种放法。