🏆2025六年级YMO复赛线下试卷
创建时间:2025-08-26 13:01:17
年份:2025
年级:六年级
杯赛:YMO
描述:从筛选结果创建的官方真题
题号14
中等
应用题
第1题【单选题】
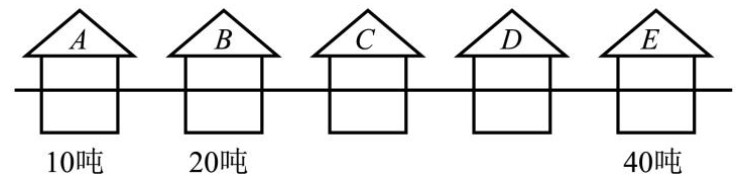
1.在小红去培训班的路上, 看到在一条公路上, 每隔 100 千米有一个仓库, 共有五个仓库。 A 号仓库存有 10 吨货物, B 号仓库存有 20 吨货物, E 号仓库存有 40 吨货物, 其余两个仓是空的。 现在想把所有的货物集中存放在任意一个仓库里, 如果每吨货物运输 1 千米需要 1 元运费, 那么放在( )才能使运费最少。

题号16
中等
几何图形
第2题【单选题】
一种足球的表面是由 30 多块黑色五边形皮和白色六边形皮围成的。 仔细观察足球皮的拼接方式,
想一想, 黑色皮块数和白色皮块数的比应该是( )。

想一想, 黑色皮块数和白色皮块数的比应该是( )。

题号17
困难
几何图形
第3题【单选题】
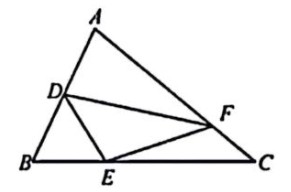
在△ABC 中,AD=
\( \frac{1}{2} \)
AB,BE=
\( \frac{1}{3} \)
BC,CF=
\( \frac{1}{4} \)
AC,△ABC 的面积是 1,求△DEF 的面积

题号18
中等
几何图形
第4题【单选题】
4.一个长方形, 如果它的长增加
\( \frac{1}{4} \)
, 宽增加
\( \frac{1}{3} \)
,那么新的长方形的面积比原来增加( )。
题号19
中等
应用题
第5题【单选题】
一项工作, 如果甲、 乙合做, 15 天可以完成; 如果甲先单独做 5 天, 剩下的乙单独做, 还需要 45 天。 现在乙先单独做 12 天, 剩下的甲单独做, 还需要( ) 天。
题号21
中等
应用题
第7题【单选题】
甲乙丙三人一起种植一批树, 分配任务时, 甲、 乙、 丙三人种植棵数之比为 1∶ 1∶ 2, 实际种植过程中, 甲、 乙、丙三人种植棵数之比为 4∶ 3∶ 5, 其中一人比原计划少种了 80 棵, 那么甲实际种了( ) 棵。
题号23
中等
数论初步
第9题【单选题】
如图所示, a、 b、c、 d、 e、 f分别是 1~10 内六个不同的自然数, 且前面标有两个箭头的每一个数恰等于箭头起点
的两数的和(如b = a + d), 那么图中c最大应为( )
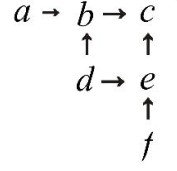
的两数的和(如b = a + d), 那么图中c最大应为( )
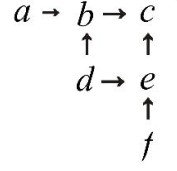
题号15
中等
数论初步
第10题【单选题】
自然数 8336, 8545, 8782 有一些共同特征, 每个数都是以 8 开头的四位数, 且每个数中恰好有两个数字相同。 这样的数共有( ) 个。
题号32
简单
计数与组合
第12题【填空题】
在一个不透明的纸箱里有除颜色不同, 其他全部相同的小球 15 个, 其中蓝球 4 个, 红球 5 个, 白球 6 个, 要想确
保摸出 2 个同色的小球, 至少要摸( ) 次。
保摸出 2 个同色的小球, 至少要摸( ) 次。
题号35
中等
应用题
第15题【填空题】
某班统计数学考试成绩, 平均分是 84.2 分, 后来发现小明的成绩是 97 分, 而错误地统计为 79 分, 重新计算后, 平均成绩是 84.6 分, 则这个班的学生人数是( ) 名。
题号36
困难
应用题
第16题【填空题】
某公司仓库里原有一批存货, 以后每天陆续有货入库, 且每天进的货一样多。 用同样的汽车运货出库, 如果每天用24 辆汽车, 5 天刚好运完; 如果每天用 18 辆汽车, 8 天刚好运完。 现在用若干辆这样的汽车运货出库, 运 4 天后, 仓库每天的进货量是原来每天进货量的 1.5 倍, 如果要求用 10 天时间运完仓库里的货, 那么至少需要( ) 辆这样的汽车(不准超载)。
题号37
中等
计算技巧
第17题【填空题】
快入冬时, 白兔和灰兔都储存了一些萝卜, 灰兔先把自家萝卜的
\( \frac{1}{4} \)
送给白兔。 白兔收到萝卜后, 觉得自己吃不完, 又
将自己现有萝卜的 \( \frac{1}{4} \) 送给灰兔。 这时两只兔子的萝卜一样多, 原来灰兔的萝卜数是白兔的( )。
将自己现有萝卜的 \( \frac{1}{4} \) 送给灰兔。 这时两只兔子的萝卜一样多, 原来灰兔的萝卜数是白兔的( )。
题号38
中等
应用题
第18题【填空题】
8.某大桥由于桥面多处破损正进行全面检修, 修了一个星期之后, 已修和未修的比是 1∶ 7, 第二个星期又修了 500 米,这时已修和未修的比是 9∶ 23, 则该大桥全长是( ) 米。
题号39
困难
数论初步
第19题【填空题】
已知 33 位数
\( \overline{4ab4ab4ab\cdots ab} \)
能被 77 整除,则三位数
\( \overline{4ab} \)
=( )。
题号31
中等
应用题
第20题【填空题】
一个人在河中游泳, 逆流而上。 在 A 处将帽子丢失, 他向前游了 20 分钟后, 才发现帽子丢了。 他立即返回去找,在离 A 处 20 千米的地方找到了帽子, 则他返回来追帽子用了( ) 分钟。
题号24
中等
应用题
第21题【问答题】
1.小华放学回家需要走 10 分钟, 小雨放学回家需要走 14 分钟, 已知小雨回家的路程比小华回家的路程多
\( \frac{1}{6} \)
, 小华每
分钟比小雨多走 12 米, 小华回家的速度是每分钟多少米?
分钟比小雨多走 12 米, 小华回家的速度是每分钟多少米?
题号25
中等
几何图形
第22题【问答题】
一个直角三角形, 两条直角边分别是 4cm 和 3cm。 以下面两种方式旋转得到立体图形(每条旋转轴垂直于底边), 旋转后图 1 的体积是图 2 体积的多少?
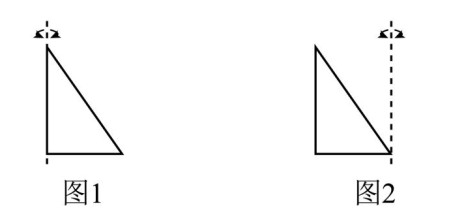
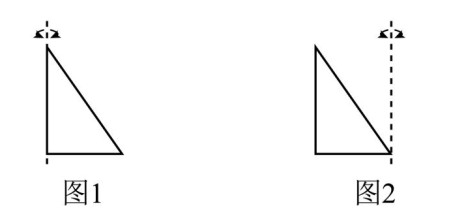
题号26
应用题
第23题【问答题】
有若干袋蓝色和黑色的玻璃球, 每个袋子中的玻璃球数量都相同, 且每个袋子中有 27%的玻璃球是蓝色的。 现在从其中一个袋子中拿走这袋玻璃球数量的一半, 且拿走的玻璃球都是黑色的, 使得蓝色玻璃球的总数占剩余玻璃球总数的 36%。 则原来一共有多少袋玻璃球?
题号27
困难
应用题
第24题【问答题】
三块牧场, 场上的草长得一样密, 而且长得一样快, 它们的面积分别是 3 公顷、 10 公顷和 24 公顷。 第一块牧场饲养 12 头牛, 可以维持 4 周; 第二块牧场饲养 25 头牛, 可以维持 8 周。 问第三块牧场上饲养多少头牛恰好可以维持 18周?
题号28
困难
应用题
第25题【问答题】
大巴和轿车都从 A 地出发驶向 B 地, 大巴与轿车的速度之比为 5∶ 6。 大巴比轿车早出发 18 分钟, 但在 AB 的中点 C
处停留了 8 分钟, 轿车则不停的驶向 B 地。 如果大巴和轿车的速度都不变, 大巴将比轿车晚 2 分钟到达 B 地。
(1) 轿车出发多少分钟后追上大巴?
(2) 如果轿车追上大巴后, 速度增加 \( \frac{1}{6} \) , 且轿车到达 B 地后立即原路返回 A 地, 当轿车再次与大巴相遇时, 大巴已经
行驶了全程的几分之几?
处停留了 8 分钟, 轿车则不停的驶向 B 地。 如果大巴和轿车的速度都不变, 大巴将比轿车晚 2 分钟到达 B 地。
(1) 轿车出发多少分钟后追上大巴?
(2) 如果轿车追上大巴后, 速度增加 \( \frac{1}{6} \) , 且轿车到达 B 地后立即原路返回 A 地, 当轿车再次与大巴相遇时, 大巴已经
行驶了全程的几分之几?