第1题【填空题】 计算: 345 × 7 × 11 × 13=_________。

第2题【填空题】 2024 年 8 月 4 日为星期日，2024 年从 8 月 1 日到 12 月 31 日，星期日的总天数为_________。

第3题【填空题】 一个被 2 除余数为 1 的自然数称为奇 (jī) 数。从 {0,1,2,3,4,5,6,7,8,9} 中选出 2 个数字 (每个数字可以重复选取) 组成两位数，最多可以得到_________个不同的两位奇数。

第4题【填空题】 红星小学三年级学生总人数是 398, 其中男生比女生少 8 人，那么，男生的总人数是_________。

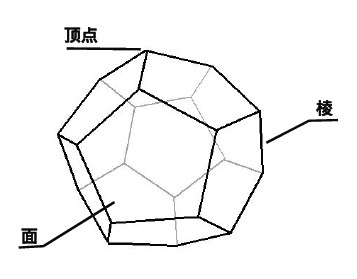
第5题【填空题】 如图所示的多面体叫做正十二面体，是 5 个柏拉图立体 (正多面体) 中的一个。这个多面体有_________个顶点、_________个面 (正五边形) 与_________条棱。

第6题【填空题】 用 \( 2^2 \) 表示2x2 , \( 2^3 \) 表示2×2×2,… 如果 \( 2^{\Delta}=1024 \) , 那么 \( \Delta \) =_________。

第7题【填空题】 有两个自然数，第一个被 7 除余 2, 这两个数的乘积被 7 除余 3, 则第二个数被 7 除余_________。

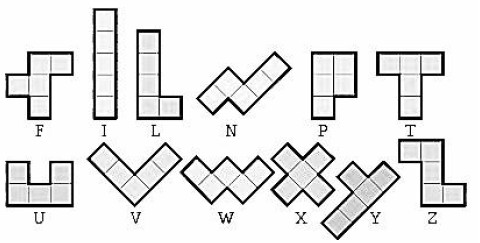
第8题【填空题】 用 5 个边长为单位长度的小正方形 (单位正方形) 可以构成如右下图所示的 5 - 联方 (在中国又称为伤脑筋十二块)。在西方国家，人们用形象的拉丁字母来标记每一个 5 - 联方。请将具有轴对称性质的 5 - 联方找出来，并将对应的拉丁字母标记写在下面:__________________。

第9题【填空题】 篮子里有足够多的苹果、梨、桃和桔子，现有 25 个小朋友，如果每个小朋友都从中任意拿两个不同的水果，那么，每个小朋友可以有_________种不同的水果选择方式，至少有_________个小朋友的选择方式是相同的。

第10题【填空题】 古希腊数学家们将一些自然数按照以下方式与三角形联系起来：并将这些数称为三角形数（1,3,6,10,15…）。

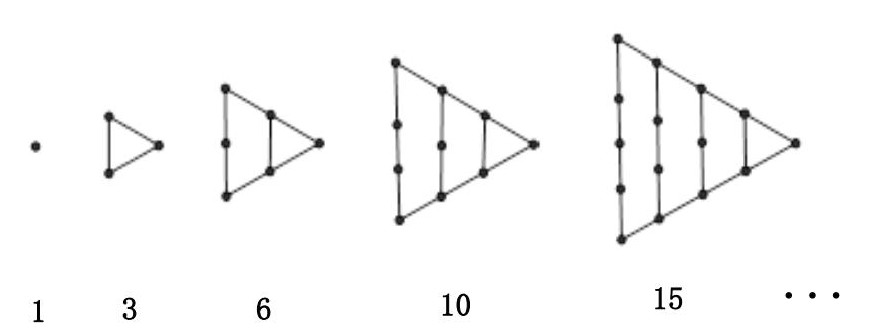
1796 年，德国数学家高斯证明：任何一个自然数都可以表示为最多 3 个三角形数的和。比如 \( 2=1+1 \) , \( 4=3+1 \) , \( 5=3+1+1 \) 等。请将 60 表示为最多 3 个三角形数的和:_________。

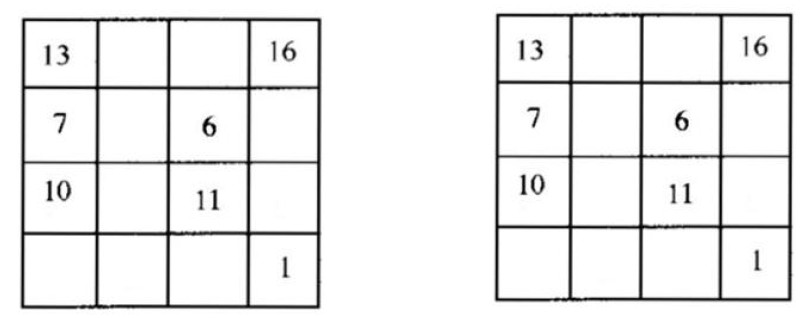
第11题【填空题】 将自然数 1 到 16 排成 4×4 的方阵，每行每列以及对角线上数的和均相等，这样的方阵称为 4 阶幻方。南宋数学家杨辉是最早系统研究幻方的中国古代数学家。请根据下面已经给出的数字，填出两个不同的 4 阶幻方。

第12题【填空题】 在印度河畔的圣庙前，一块黄铜板上立着 3根金针，针上穿着很多金盘。梵天创世时，在左边的针上穿了由大到小的 64 片金盘，他要求人们按照 “每次只能移动一片，而且小的金盘必须永远在大的金盘上面” 的规则，将所有的 64 片金盘移动到右边的金盘上面。他预言，当所有 64 片金盘都从左边的金针移动到右边的时候，宇宙就会湮 (yān) 灭。
这就是汉诺塔 (Tower of Hanoi) 的故事。

(1) 如果左边的金针上只有 3 片金盘，那么，最少需要移动多少次才能完成任务？如果有 4 片呢？(你的答案分别是:___________________________)
(2) 如果有 4 片金盘处于如图所示的状态，则最少需要移动多少次才能完成任务？(你的答案是:___________________________)。