第1题【填空题】 计算: \( 2 \frac {1}{4} \div\left (1.2+\frac {3}{5}\right) × 0.8= \) ______。

第2题【单选题】 下列各图中阴影部分面积最大的是 ( )

第3题【填空题】 一个三位数，除以 7 余 \( 6 \) , 除以 8 余 7, 除以 9 余 8, 这个三位数是

第4题【填空题】 游乐园里打靶每人次收费 3 元，钓鱼每人次收费 2 元｡周日玩打靶和钓鱼的人次之比为 2︰9, 游乐园共收费 504 元，那么这天玩打靶的有________人次｡

第5题【单选题】 如图，正方形中的圆与正方形外的圆的面积比是 ( )｡

第6题【填空题】 有 15 个大于 0 的不同奇数，99 是其中之一，2025 也是其中之一且是最大的一个｡如果这 15 个奇数中任意 8 个数的和都大于其余 7 个数的和，那么这 15 个数中最小的两个数之和是

第7题【单选题】 下列各数中最大的是 ( )｡

第8题【填空题】 算式 \( \underbrace {888\cdots8}_{2025 个 8}\div777 \) 的余数是________。

第9题【填空题】 有甲乙丙三杯重量相等的溶液，它们的浓度分别是 20%,18%,30%, 依次将甲乙丙溶液的 \( \frac {1}{4} \) 、 \( \frac {1}{3} \) 、 \( \frac {1}{2} \) 倒入第四个空杯子中，第四个杯子中溶液的浓度是________%｡

第10题【填空题】 一个边长为 2 厘米的等边三角形 ABC, 沿直线滚动 2025 次，顶点 A 经过的路程共________厘米｡(圆周率 π 取 3)

第11题【填空题】 新年到了，希希设计了一个乘法竖式谜，这个竖式的计算结果最大是_________。

第12题【填空题】 从下图中同时选出一个小灰格和一个小白格，使得这两个小格既不在同一行也不在同一列，共有________种选法｡

第13题【填空题】 公园中共有银杏树和梧桐树共 1000 棵，且银杏树的 \( \frac {2}{7} \) 比梧桐树的 \( \frac {1}{6} \) 多 36 棵。那么银杏树有________棵｡

第14题【填空题】 某公司新年晚会，参加抽奖活动的人有 \( \frac {1}{7} \) 抽到四个礼品，有 \( \frac {1}{4} \) 抽到三个礼品，有 \( \frac {1}{3} \) 抽到两个礼品，其余的抽到一个礼品｡若不到 100 人参加抽奖活动，那么有________人抽到一个礼品｡

第15题【填空题】 如图，正八边形的面积为 100, 那么阴影部分的面积为_______。

第16题【填空题】 三个连续奇数 A、B、C 满足 \( \frac {C}{36}+\frac {B}{132}+\frac {A}{198}=2.0\dot {2}\dot {5} \) , 则 \( A+B+C= \) _______。

第17题【填空题】 若 \( 1+\frac {1}{7+\frac {1}{2+\frac {1}{A+\frac {1}{1+\frac {1}{1+\frac {1}{4}}}}}}=\frac {310}{273} \) , 则 A=________。

第18题【填空题】 十进制数 n 为 100 到 500 之间的自然数，将 n 化为二进制后书写形式为 “回文数”(正读反读都相同), \( n+1 \) 化为四进制后也是 “回文数”, \( n+2 \) 化为六进制后也是 “回文数”｡那么十进制数 n 是_________。

第19题【填空题】 爸爸和妈妈都从北京出发到距离 2025 千米的某城市出差，爸爸先乘坐高铁，后改为乘汽车，妈妈则直接乘坐飞机，最终两人同时到达｡已知爸爸比妈妈早出发 3 小时 56 分，高铁的平均速度为 300 千米 / 时，汽车的平均速度为 80 千米 / 时，飞机的平均速度为 675 千米 / 时，那么爸爸乘坐汽车行了________千米｡

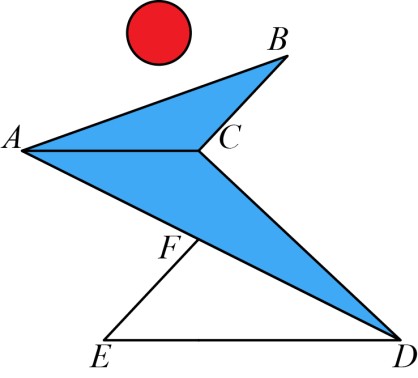
第20题【填空题】 下图是某校运动会的会标，图中 \( AC\parallel DE \) , \( BC\perp CD \) ,F 是 AD 中点，且 \( \angle CDE=\angle E \) ｡若 \( AC=30 \) , \( BC=20 \) , \( CD=50 \) , \( DE=55 \) , 则图中两个阴影三角形的面积之和是_________。

第21题【填空题】 一个数的所有因数中有 2025 个是 5 的倍数，有 675 个不是 5 的倍数，那么所有满足该条件的数的最大公因数是_________。

第22题【填空题】 有一个多位数 (至少两位), 从左到右的第一个数字等于这个多位数中奇数数字的个数，第二个数字等于这个多位数除以 2 的余数，第三个数字等于这个多位数除以 3 的余数，第四个数字等于这个多位数除以 4 的余数，……｡如果这个多位数不超过 2025, 那么这个多位数有________种可能｡

第23题【填空题】 原计划由甲、乙、丙三个车队按 11∶13∶10 的比例为工地运送一批建材｡实际上，由于三个车队效率发生变化，丙车队比原计划多运输了 35 吨建材，最终三个车队运送建材的比例为 31∶36∶35｡这批建材共________吨｡

第24题【填空题】 两个非零自然数相加等于 2025, 在相加的过程中发生进位，这样的加法算式有________个 ( \( a+b \) 和 \( b+a \) 视为同一个加法算式)

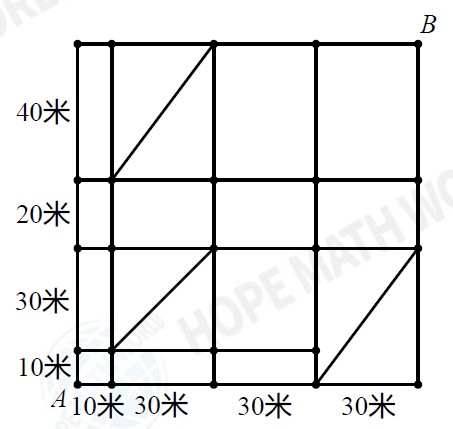
第25题【填空题】 如图，每条线段都代表路线，人们在行走的时候不能在线段中掉头，线段长度已在图上标出｡现要在图中设置一个打卡点 C, 在从 A 行走到 B 的过程中必须经过 C 点，使得在走最短路径的情况下从 A 到 B 共行走至少 200 米，那么一共可以在________个位置设置打卡点 C。