第1题【填空题】 计算： \( 0.13×5×0.31×73×137 \) = ________.

第2题【填空题】 自然数 1111111111111111 被 8 除余数为________.

第3题【填空题】 将 2024 分拆成 300 个质数之和，要求其中最大的质数尽可能小，那么这个最大质数是________.

第4题【填空题】 自然数 6 的所有因数为 1，2，3，6，其中，1，2，3 称为 6 的真因数。类似地，任何自然数除自身之外的因数都称为它的真因数。注意到 1+2+3 = 6，像 6 这样，如果一个自然数的所有真因数加起来等于它自己，这个自然数就被称为完美数（或完全数），6 就是最小的完美数. 28，496，8128 也是最早知道的几个完美数。3 是 6 的奇质因数，请分别写出 28，496 的奇质因数是________.

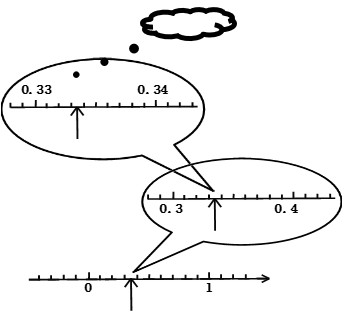
第5题【填空题】 如图所示的直线上，我们将 “01 线段” 10 等分，竖直箭头所指的数，落在从左至右的第 4 个线段上（不含线段的端点），继续将这个线段 10 等分，这个数仍然落在从左至右的第 4 个线段上，…… 可以一直这样操作下去。那么，这个数用小数表示为________，用分数表示为________.

第6题【填空题】 下图是一个街道的示意图，实线表示道路。从 B 到 A，只能向右或向上或右斜上方沿着道路前进，则一共有________种不同的走法.

第7题【填空题】 一副扑克包括大小王在内共 54 张，其中，红桃、黑桃、梅花、方块 4 种花色的牌各 13 张。在一副扑克中任意抽取至少________张牌，才能保证 4 种花色都被抽到，而任意抽取 2 张牌，恰好抽到大王与小王的可能性（概率）为________（用最简分数表达）.

第8题【填空题】 老师在黑板上写了 13 个自然数，让陶陶计算平均数（精确到百分位）. 陶陶计算得到的答数是 10.93，老师说百分位上的数字错了，其它数字都对。那么，正确答数应该是________.

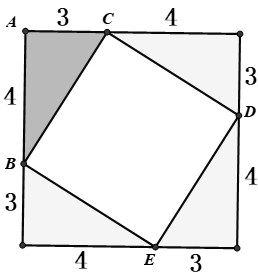
第9题【填空题】 将直角边分别为 4 和 3 的 4 个直角三角形，按照如图所示的方式组成一个边长为 7 的正方形，在这个图形中，四边形 BCDE 的面积为________，BC 的长为________，点 A 到 BC 边的距离为________.

第10题【填空题】 在中国古代的历法中，甲、乙、丙、丁、戊、己、庚、辛、壬、癸被称为 “十天干”，子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥叫作 “十二地支”。十天干和十二地支进行循环组合：甲子、乙丑、丙寅、...... 一直到癸亥，共得到 60 个组合（如下表），称为六十甲子。如此周而复始用来纪年的方法，称为甲子纪年法。

01 甲子　11 甲戌　21 甲申　31 甲午　41 甲辰　51 甲寅；
02 乙丑　12 乙亥　22 乙酉　32 乙未　42 乙巳　52 乙卯；
03 丙寅　13 丙子　23 丙戌　33 丙申　43 丙午　53 丙辰；
04 丁卯　14 丁丑　24 丁亥　34 丁酉　44 丁未　54 丁巳；
05 戊辰　15 戊寅　25 戊子　35 戊戌　45 戊申　55 戊午；
06 己巳　16 己卯　26 己丑　36 己亥　46 己酉　56 己未；
07 庚午　17 庚辰　27 庚寅　37 庚子　47 庚戌　57 庚申；
08 辛未　18 辛巳　28 辛卯　38 辛丑　48 辛亥　58 辛酉；
09 壬申　19 壬午　29 壬辰　39 壬寅　49 壬子　59 壬戌；
10 癸酉　20 癸未　30 癸巳　40 癸卯　50 癸丑　60 癸亥。

我们知道，公元 2024 年是甲辰年，那么，用甲子纪年法，公元 1949 年是________年，公元 3000 年是________年.

第11题【填空题】 有 4 个自然数，从其中任意选取 3 个数求和，可以而且只能得到 32，33，34，那么，原来的 4 个自然数分别是________.

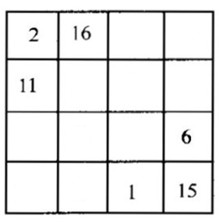
第12题【填空题】 将自然数 1 到 16 排成 4×4 的方阵，每行每列以及对角线上数的和均相等，这样的方阵称为 4 阶幻方。南宋数学家杨辉是最早系统研究幻方的中国古代数学家，请将下面他给出的 4 阶幻方补充完整：